
|
Plasma Theory Group
|

| 
| 
|
Research
- Magnetic Fusion: Simulation and Theory
- L-H Transition and Tokamaks -- Antonsen, Dorland, Drake, Guzdar, Hassam, Liu, Novakovski, Rogers
- b Limit Disruptions in Tokamaks -- Kleva, Guzdar
- Theory of Intense Laser Plasma Interactions -- Antonsen
- Magnetic Reconnection -- Drake, Rogers, Shay
- Centrifugally Confined Plasmas -- Hassam
- Space Plasma Theory -- Guzdar
- Theory and Simulation of High Power Coherent Radiation Sources -- Antonsen
MAGNETIC FUSION: SIMULATION AND THEORY
L-H Transition and Tokamaks
Antonsen,
Dorland,
Drake,
Guzdar,
Hassam,
Liu,
Novakovski,
Rogers
The tokamak is the primary device which has the potential for achieving thermonuclear fusion in a controlled environment. Over the last decade, very significant advances have been made on this device. New, improved modes of confinement have been found which have profound implications in the design of fusion reactors. A first principles understanding of the cause of these improved modes of confinement has been one of the major areas of research being pursued by the Plasma Theory Group at the University of Maryland.
The first mode of improvement in confinement, observed on devices all over the world, is the so-called L-H transition. In a tokamak heated by a neutral beam to achieve high plasma temperatures, the preliminary results were discouraging. It was observed that as the neutral beam power was increased, the particle and energy confinement times decreased. This mode of operation of the tokamak was referred to as the low (L) mode. This did not bode well for achieving the goals of thermonuclear fusion. However, with the further increase in input power, the discharge made a dramatic transition to a good confined mode, the high (H) mode. The improvement in confinement has been attributed to the generation of shear flow in the edge region of tokamaks, which creates a transport barrier.
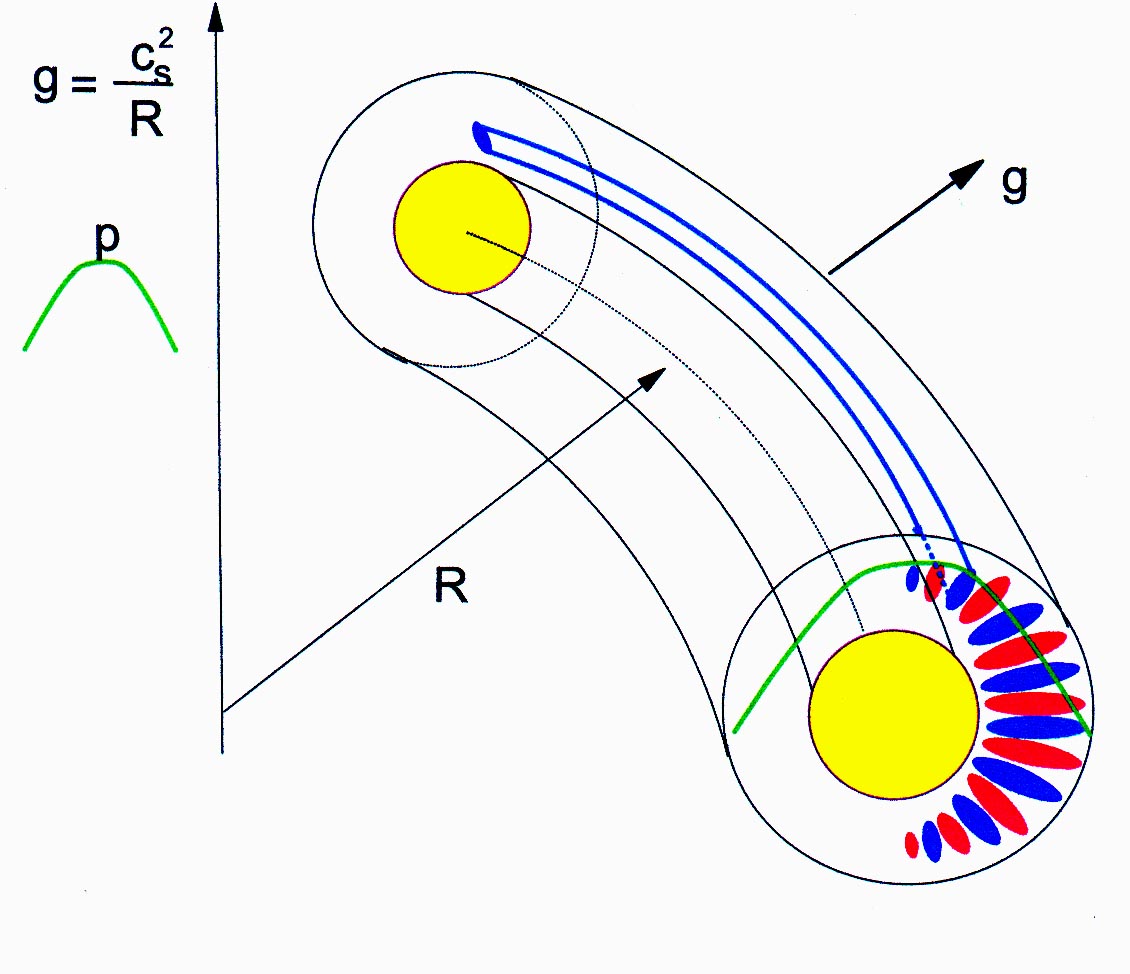
The Maryland Plasma Theory Group has made significant contributions in two areas relevant to the understanding of the L-H transition. By doing detailed 3D simulations of the edge region of the plasma, which have progressively been refined over the last few years, the cause of the anomalous transport, which lead to the poor confinement in the L mode phase, has been identified. The edge is prone to short scalelength convection due to the effective gravity arising from the toroidal curvature of the field lines. The pressure gradient and the gravity on the outside are unfavorable for stability. On the other hand, the pressure gradient on the inside is reversed and the plasma is stable. Thus this "ballooning" instability leads to enhanced particle and energy transport. The strong asymmetry in the transport is an important consequence of the theory, directly verified on some tokamaks which have the necessary diagnostics to measure the transport and fluctuations around the poloidal periphery.
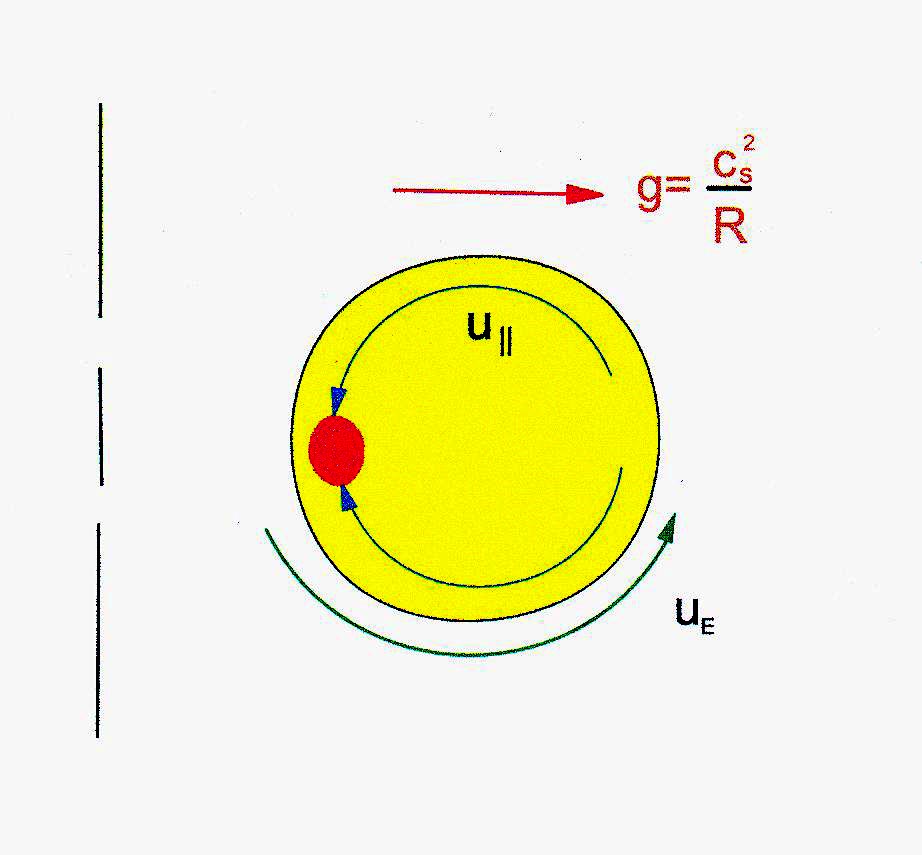
Another area related to the L-H transition problem is to develop an understanding of the generation of shear flow. Here again the Plasma Theory Group at Maryland has advanced a very plausible scenario to explain why the edge spins up when the temperature exceeds a critical temperature. The second figure shows that, due to asymmetric transport, the density varies on the magnetic flux surface. The local enhancement of the density on the inside (depicted by a blob) has a tendency to "fall" under the influence of the effective gravity. However, there are dissipative effects which dampen the fall. As the temperature increases, the damping weakens and the fall causes the blob to spin around in the poloidal direction. This spin-up confined to the edge strongly suppresses the ballooning, thereby giving rise to a transport barrier which improves the confinement. This research has led to a proposed scenario in which the spin-up is induced by neutral beams, thereby facilitating the onset of improved confinement.
Another possible mechanism for transport barrier formation is also being pursued by members of the Plasma Theory Group, based on recent results from 3-D numerical simulations of edge turbulence in the presence of a fueling source. In response to the fueling, the edge plasma gradients in the simulation tend to steepen. This normally leads to an intensification of turbulence and a corresponding increase in the transport of particles and heat, thereby allowing the system to come into a new equilibrium with the source. In regimes of higher temperature (specifically, regimes of high MHD ballooning parameter a), however, the simulations show this dependence of the transport on the gradient can become reversed, making it impossible for such an equilibrium to be maintained. The result is a spontaneous steepening of the gradients that resembles the LH transition.
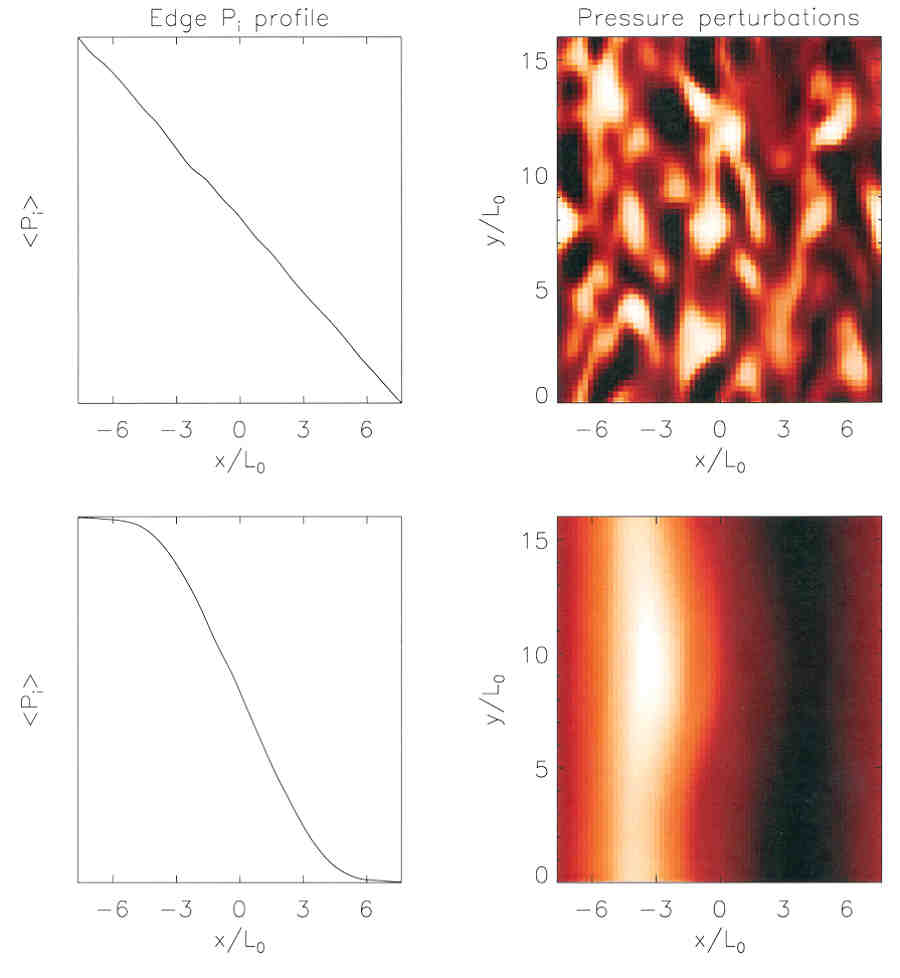
3-D Simulation of L/H Transition and Edge Pedestal
Another area of research in which the group plays a significant role is addressing the issues of magnetohydrodynamic (MHD) stability of high density and high temperature reactor-relevant plasmas. Achieving high density in the tokamak is important for making fusion power a commercially viable alternative. Such plasmas tend to develop equilibrium pressure and current profiles very different from present-day devices. The members of the Plasma Theory Group here have developed efficient numerical codes which can readily address these important issues. Results from the group indicate that some of the proposed high density equilibria may be violently unstable to a class of MHD modes which are not present in present-day low density devices.
This research is supported by the U.S. Departent of Energy.
b Limit Disruptions in Tokamaks
Kleva, Guzdar
The most serious impediment to the practical utilization of tokamaks as fusion reactors is the limitation on the plasma thermal pressure imposed by disruptions. The ratio b of the thermal pressure to the pressure of the confining magnetic field provides a measure of the efficiency of a magnetic confinement fusion reactor. Operation at high b is very desirable because it yields a large fusion reaction rate relative to the cost of the confining magnetic field. However, experimental attempts to increase the ratio b beyond a critical limit bc have been thwarted by an abrupt, catastrophic loss of confinement. Not only do these disruptions limit b and, therefore, limit the efficiency of a tokamak, but the disruptions themselves can cause serious damage to the reactor.

p>
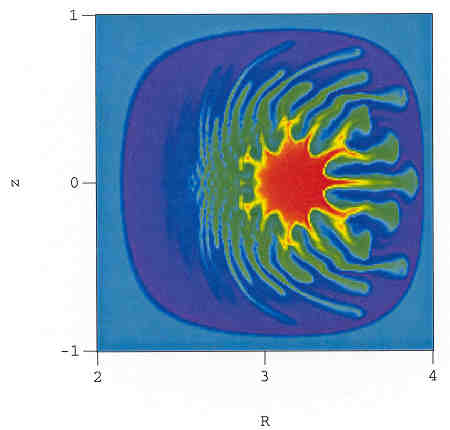
The first figure shows three-dimensional isosurfaces of the pressure as the instability develops along ridges dominantly aligned along the ambient magnetic field. The next figure is a poloidal projection of the pressure that shows the hot plasma fingers as they reach the wall. Our nonlinear simulations of tokamak stability reproduce the salient
features of the disruptive loss of confinement. High b toroidal
equilibria are linearly unstable to ballooning modes that grow on the
pressure gradient on the large R side of the magnetic axis, where
R is the major radius of the torus. The convection cells associated
with the unstable ballooning modes transport the thermal energy toward
the wall at large R in hot plasma ridges whose two-dimensional
projection in the poloidal plane resembles fingers. As the hot central
plasma is transported out in R in fingers, the average pressure
gradient is reduced so that it no longer completely balances the
Lorentz force of the confining magnetic field. As a result, there is a
small net inward force in R caused by the unbalanced Lorentz
force. At lower bthis force generates an axisymmetric flow
that opposes the growth of the fingers to the wall at large R,
thereby stabilizing the plasma nonlinearly and maintaining
confinement. However, as b increases the growth rate of the
plasma fingers towards the wall becomes so rapid that there is
insufficient time for the self-consistently generated axisymmetric
flow to halt their progress before they strike the wall, and
confinement is lost.
Recent papers dealing with disruptions in tokamaks:
-
b Limit Disruptions in Tokamaks, R.G. Kleva and P.N. Guzdar,
Phys. Rev. Lett. 80, 3081 (1998).
-
Nonlinear Stability Limit in High b Tokamaks, R.G. Kleva and
P.N. Guzdar, Phys. Plasmas 7, 1163 (2000).
This research is supported by the U.S. Department of Energy.
THEORY OF INTENSE LASER PLASMA INTERACTIONS
Antonsen
Channeling of intense optical fields in plasmas is a rapidly developing scientific area, with a number of possible applications including x-ray generation, harmonic conversion and electron acceleration. In the context of laser plasma accelerators, intense, ultrashort pulses of laser light are injected into a plasma and create a wake field that can be used to accelerate particles. The major challenge is to produce a wake which is strong enough and coherent over a sufficiently large distance to accelerate particles to high energy.
Many nonlinear physical processes can be expected to affect the propagation of these intense pulses, and their study requires a synthesis of nonlinear optics and basic plasma physics. In particular, intense laser pulses are subject to self-channeling and Raman instabilities. Self-channeling occurs because the oscillating motion of plasma electrons in the presence of the laser field is relativistic for intense pulses. The increase in the effective mass of the electrons which accompanies their relativistic oscillations results in a change in the index of refraction of the plasma and consequently leads to self-guiding of the laser light. In addition, the laser light can also act to expel electrons from regions of high intensity further enhancing the channeling process. Raman instabilities occur when an intense pulse decays by creating a plasma wave and a lower frequency light wave. This usually leads to a breakup of the laser pulse. The interplay of these effects determines the distance over which laser pulses can propagate through plasmas.
Our group has been engaged in developing theory\linebreak models and numerical simulation tools to study the evolution of intense laser pulses. In addition, there is a strong link to experimental efforts conducted by Prof. H. Milchberg of the Institute for Physical Science and Technology and the Department of Electrical Engineering. The figures below show the results of a numerical simulation of laser light propagation through a preformed plasma channel.
The parameters correspond to those of a proposed experiment to be conducted in Prof. Milchberg's laboratory. Displayed are two dimensional surface plots of the laser intensity after propagation through channels with four different parameters. Visible on the trailing edge of the laser pulses are modulations corresponding to excitation of Raman instabilities. Clearly, the parameters corresponding to channel a provide for the most stable propagation.
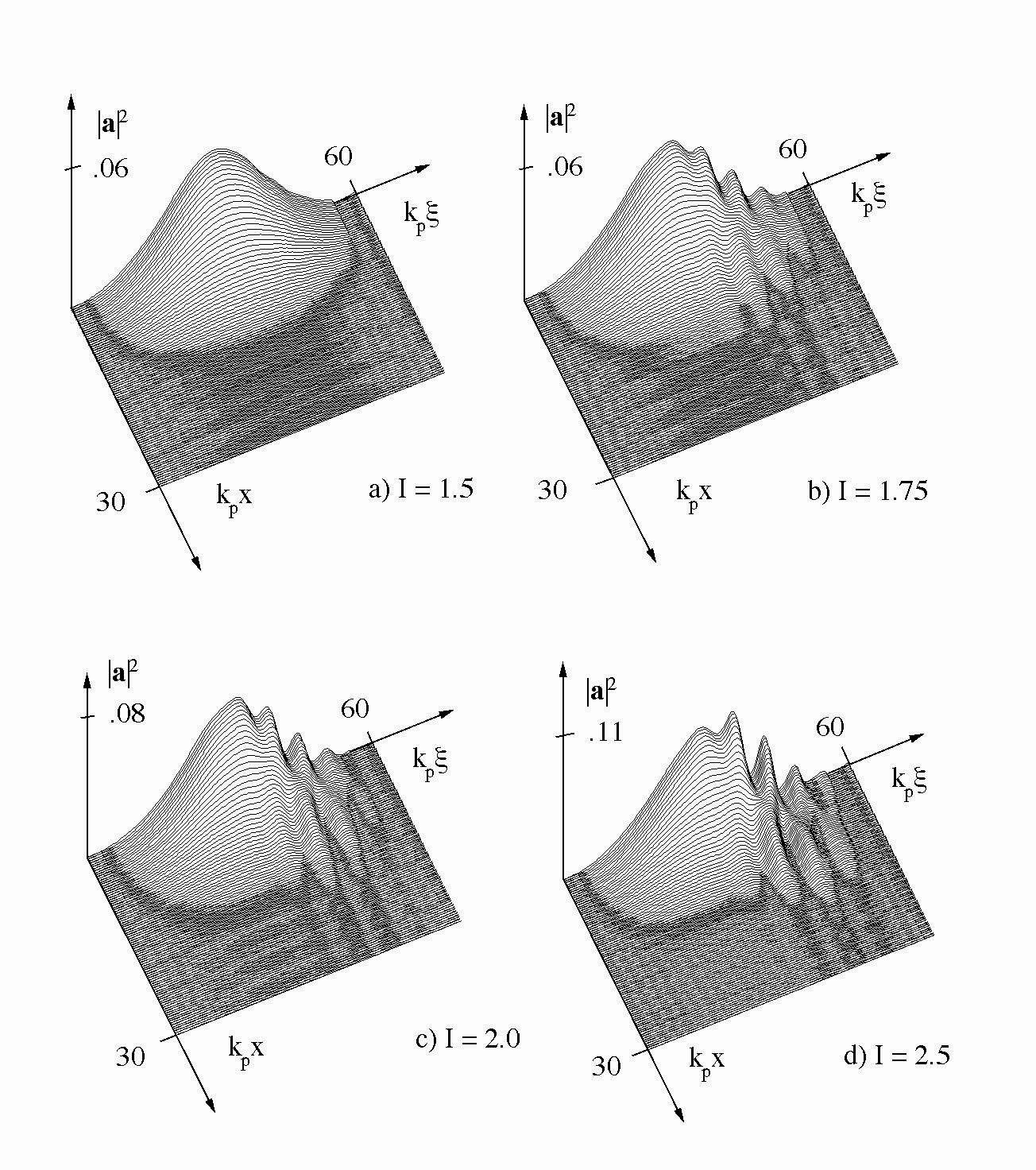
Results of a numerical simulation of laser light propagation through a preformed plasma channel.
This research is supported by the National Science Foundation.
MAGNETIC RECONNECTION
Drake, Rogers, Shay
 Solar flares, storms in the earth's magnetosphere and disruptions in
laboratory fusion experiments are examples of large scale explosive
events which occur in plasma systems. The magnetic field is the source
of free energy driving these phenomena. This magnetic energy can be
released in locations where the magnetic field reverses
direction. That is, the magnetic field can self-annihilate in these
region and transfer its energy to plasma flows and intense, high
energy beams. A major scientific challenge has been to explain the
short time scales of this energy release. It is well established that
the magnetic energy is released by magnetic reconnection, in which
magnetic field lines in opposing directions cross link, forming a
topological x-line. The topological change in the magnetic field
required to form the x-line requires a breakdown in the ideal
"frozen-in" flux condition, which occurs at small scales. As a result,
magnetic reconnection occurs in narrow boundary layers. This topic
is
considered to be one of the two or three most important topics in
plasma physics over the past thirty years because it occurs in so many
varied environments and because the dependence of a large-scale,
explosive phenomenon on the kinetic behavior at small scale has
intrinsic interest.
Solar flares, storms in the earth's magnetosphere and disruptions in
laboratory fusion experiments are examples of large scale explosive
events which occur in plasma systems. The magnetic field is the source
of free energy driving these phenomena. This magnetic energy can be
released in locations where the magnetic field reverses
direction. That is, the magnetic field can self-annihilate in these
region and transfer its energy to plasma flows and intense, high
energy beams. A major scientific challenge has been to explain the
short time scales of this energy release. It is well established that
the magnetic energy is released by magnetic reconnection, in which
magnetic field lines in opposing directions cross link, forming a
topological x-line. The topological change in the magnetic field
required to form the x-line requires a breakdown in the ideal
"frozen-in" flux condition, which occurs at small scales. As a result,
magnetic reconnection occurs in narrow boundary layers. This topic
is
considered to be one of the two or three most important topics in
plasma physics over the past thirty years because it occurs in so many
varied environments and because the dependence of a large-scale,
explosive phenomenon on the kinetic behavior at small scale has
intrinsic interest.
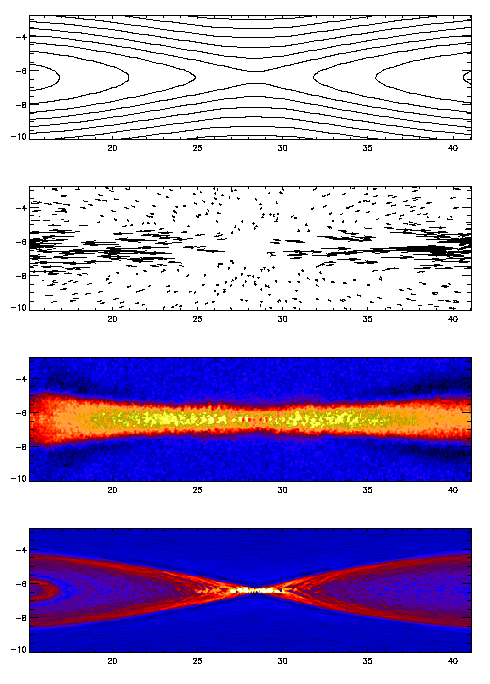
Key discoveries in magnetic reconnection made center around the role of whistler waves in driving and controlling magnetic reconnection. Traditionally it was believed that the Alfven wave played the key role in driving reconnection. At small scales, however, electron and ion motion decouple and the dynamics is controlled by whistler waves. The whistler waves fundamentally alter the reconnection process, causing the release rate of magnetic energy to be insensitive to the mechanism which breaks the frozen-in condition. The figure on the right shows the results of a computer simulation of magnetic reconnection. From top to bottom are the magnetic field lines, the plasma flows, and the ion and electron currents.
Recent papers dealing with collisionless magnetic reconnection are:
- The role of electron dissipation on the rate of collisionless magnetic reconnection, M. A. Shay and J. F. Drake. Demonstrates that the whistler wave renders the reconnection rate insensitive to the mechanism which breaks the frozen-in condition using analytical calculations backed by particle simulations.
- The scaling of collisionless
magnetic reconnection for large systems , M. A. Shay, J. F. Drake, B. N. Rogers, and R. E. Denton. Demonstrates that the dynamics of
the whistler wave leads to a scale invariant rate (and therefore
Afvenic rate) of magnetic reconnection even at very large scales.
This research is supported by the National Science Foundation and the National Aeronautics and Space Administration.
CENTRIFUGALLY CONFINED PLASMAS
Hassam
Centrifugal forces from supersonic plasma rotation can be used to augment the usual magnetic confinement of plasmas. When optimized, this "knob" results in a device that features several advantages over conventional approaches.
The idea rests on two prongs: first, centrifugal forces can be used to contain plasmas to desired regions of appropriately shaped magnetic fields; second, the accompanying large velocity shear can stabilize even MHD instabilities. If these ideas are workable, the resulting coil configuration is simple and there are no substantial plasma currents.
As far as transport goes, the velocity shear can also quell microturbulence, leading to fully classical confinement as there are no neoclassical effects. Classical parallel electron transport then determines the confinement time. These losses are minimized by a large Pastukav factor resulting from the deep centrifugal potential well. At Mach 4-5, the Lawson Criterion is accessible. We are developing the theory of this concept.
In addition, an experiment has been proposed at the University of Maryland (Maryland Centrifugal Torus, MCT). The central goal of the MCT experiment will be to obtain MHD stability from velocity shear. Specifically, it will be determined how much, if any, toroidal field is necessary to suppress residual wobbles and convection from the interchange. Previous experiments were probably MHD convection limited and did not have a toroidal field. In addition, the MCT experiment will feature a plasma of elongation 6-8, which should reduce the interchange growth rate and so reduce Mach number requirements.
This research is supported by the U.S. Department of Energy.
Theory Homepage • IPR Homepage
Webpage maintained by Dorothea F. Brosius
Created 4/22/99 by DFB
Modified 7/28/00 by DFB